|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Дележ, отвечающий аксиомам Нэша
Сделки с побочными платежами
Согласно сделанному выше предположению (см. замечание в "Сделки без побочных платежей" , функции выигрышей сторон можно интерпретировать как линейно трансферабельные полезности. Однако в предшествующем рассмотрении (при определении допустимого множества S из (14.6)) было введено ограничение, запрещавшее обмен полезностями между сторонами. Теперь мы рассмотрим случай, когда такого ограничения нет. При этом передача полезностей от одного игрока к другому не изменяет их суммарной полезности.
Допустимость обмена полезностями расширяет круг возможных договоренностей
игроков, поскольку становятся реализуемыми сделки  ,
если они удовлетворяют условию
,
если они удовлетворяют условию
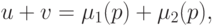 |
( 15.23) |
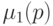 ,
, 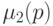 соответственно из (14.2)-(14.4).
Т.е. получаемая сторонами суммарная полезность из правой
части равенства (15.23) может быть перераспределена между ними в согласованную
пару (u,v) за счет побочных платежей.
соответственно из (14.2)-(14.4).
Т.е. получаемая сторонами суммарная полезность из правой
части равенства (15.23) может быть перераспределена между ними в согласованную
пару (u,v) за счет побочных платежей.Это обстоятельство определяет заинтересованность сторон в согласованной реализации такой стратегии p+ из (14.2), которая максимизирует суммарную полезность:
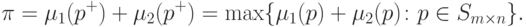 |
( 15.24) |
 (15.24)
эквивалентна линейной программе вида
(15.24)
эквивалентна линейной программе вида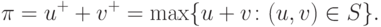 |
( 15.25) |

Заметим, что в случае, когда допустимое множество S
представляет собой плоский многоугольник (как это имеет место в случае биматричных
игр), решение задачи (15.25) достигается в одной из неулучшаемых вершин этого
многоугольника. Т.е. максимальная возможная величина суммарной
полезности  может быть достигнута в чистых стратегиях.
может быть достигнута в чистых стратегиях.
Исходя из реализуемости максимального значения из (15.22) и руководствуясь основными идеями схемы Нэша, перейдем к вопросу об оценке сделки (u+,v+), которую будут готовы согласовать стороны P1 и P2 с учетом побочных платежей. При этом будем полагать, что
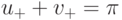 |
( 15.26) |
 |
( 15.27) |
 .
.При этих предположениях стороны могут согласовать любую сделку из множества
 |
( 15.28) |
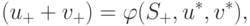 |
( 15.29) |
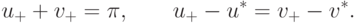
![u_{+} = \frac{1}{2} \left[\pi + (u^\ast - v^\ast)\right]\!,\quad
v_{+} = \frac{1}{2} \left[\pi - (u^\ast - v^\ast)\right]\!,](/sites/default/files/tex_cache/4ed1048f4d9d6567214e99efae3c71cc.png) |
( 15.30) |
Пример 3.2. Вернемся к задаче о строительстве с долевым участием (см. "Стратегическое равновесие в 2 x 2 играх" ) и введем новые платежные функции сторон, представленные в табл. 3.2. Пары чистых стратегий ( i=1, j=1 ) и ( i=2, j=2 ), соответствующие двум возможным районам строительства гостиничного комплекса с долевым участием, по-прежнему обладают свойствами устойчивости и эффективности. Однако, как мы уже указывали, при этом нет механизма выбора конкретной пары. Матрицы отражают также, что в случае отказа от строительства комплекса стороны используют свои средства для развития системы предприятий обслуживания. При этом сторона P1 несет убытки, если она развивает предприятия в "своем" (достаточно насыщенном услугами) районе Р1.
Допустимое множество S для рассматриваемой задачи представлено на рис. 3.9.
Точка  ,
оцененная в соответствии с выражениями (14.7), (14.10)
и (11.10), также отмечена на рис. 3.9. Дележ
,
оцененная в соответствии с выражениями (14.7), (14.10)
и (11.10), также отмечена на рис. 3.9. Дележ
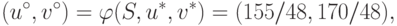
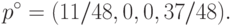
Далее, (u+,v+)=(3,4), 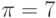 и,
согласно (15.30), (u+,v+)=(91/24,77/24). Т.е. (в случае договоренности)
стороны согласованно реализуют пару чистых
стратегий ( i=2, j=2 ), и затем вторая сторона
выплачивает первой стороне часть своего выигрыша, которой соответствует
полезность
и,
согласно (15.30), (u+,v+)=(91/24,77/24). Т.е. (в случае договоренности)
стороны согласованно реализуют пару чистых
стратегий ( i=2, j=2 ), и затем вторая сторона
выплачивает первой стороне часть своего выигрыша, которой соответствует
полезность 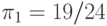 .
.



